Модели и методы линейного программирования. Модель линейного программирования

Рассмотренные выше модели можно отнести к разряду статических моделей линейного программирования, поскольку в них временной интервал был фиксирован. Если возникает необходимость найти решение для другого временного интервала, то нужно заново вводить данные в модель и производить новую оптимизацию. Иначе говоря, в подходе, рассмотренном выше, предполагалось, что все временные интервалы являются независимыми и для каждого временного интервала должна решаться своя задача оптимизации.
В динамических моделях рассматривается поведение системы на нескольких временных интервалах, а поиск решения производится один раз, оптимизируя поведение модели на всех временных интервалах сразу.
Динамические модели являются более реалистическими и более адекватно описывают многие производственные ситуации. Зависимость принятия решения от поведения системы во времени делает динамические модели исключительно полезным методом экономического анализа, но они оказываются значительно сложнее статических по своей постановке, содержат, как правило, большое число переменных, требуют определенного навыка при составлении табличной модели.
В качестве примера рассмотрим практически значимую модель управления производственными запасами (другое название этой модели – многофазовые модели управления запасами ). Для общности результатов мы не будем присваивать параметрам числовые значения. После построения модели можно будет задать явные значения параметров и получить численное решение.

Пример 3.10
Рассмотрим химическую фирму, производящую полиуретан. Производитель имеет заказы на поставку полиуретана в количестве d i тонн в месяц на ближайшие четыре месяца (i=1,2,…,4). Пусть затраты на производство одной тонны полиуретана составляют C i тыс. рублей, а максимальный объем производства полиуретана по месяцам ограничен и равен K i тонн в месяц. Производственная фирма имеет возможность хранить продукцию на складе, причем стоимость хранения одной тонны продукции за месяц составляет n i тыс. рублей. На начальный период времени запас полиуретана на складе составлял L 0 тонн. Менеджеру компании требуется составить план производства полиуретана по месяцам, который бы обеспечил выполнение заказов при минимальной стоимости производства и хранения продукта.
Решение
Заметим, что если бы не было возможности хранить продукцию на складе, то задача разбилась бы на четыре независимые статические задачи и потеряла бы для нас всякий смысл.
Составим уравнение материального баланса, позволяющего вычислить количество продукции, хранящееся на складе в течение i-го месяца. Пусть x i – количество полиуретана, произведенного в i-й временной период. Тогда в течение первого месяца товарный запас на складе будет равен L 1 =L 0 +x 1 -d 1 . Товарный запас второго месяца

Продолжая этот процесс, легко получить общую формулу товарных запасов для любого временного интервала :

. (3.24)
После того как мы вывели уравнение (3.24), описывающее поведение товарных запасов, легко записать математическую модель задачи:

(3.25)
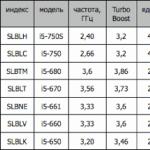
Поставленная задача (3.25) является типичной задачей линейного программирования и может быть достаточно легко решена с помощью программы Поиск решения. Используя численные значения удельных затрат производства

и необходимого объема поставок и производственных мощностей по месяцам
требуется составить оптимальный план производства полиуретана, если на первое января запас полиуретана на складе составлял 15 тонн.

Табличная модель задачи управления запасами
Табличная модель задачи после нахождения оптимального решения приведена на рис. 21.

Рис. 21. Табличная модель задачи динамического программирования

Следует сказать несколько слов и об отчете по устойчивости для этой модели, приведенном на рис. 22.

Рис. 22. Отчет по устойчивости для динамической модели

Если используется простое ограничение на значение оптимизируемых переменных (x i ≤K i в нашем случае), то в отчете по устойчивости теневые цены для этих ограничений помещаются в столбце нормированная стоимость, а информация о допустимом диапазоне теневых цен для этих ограничений не выводится. Таким образом, если увеличить на одну тонну производственные мощности в январе, то общие затраты уменьшатся на 1,7 тыс. рублей.
Требует дополнительных пояснений и столбец Целевой коэффициент отчета по устойчивости. Приведенные здесь значения Excel вычисляет самостоятельно. Смысл целевого коэффициента при переменной состоит в том, что он показывает, насколько увеличится значение целевой функции при увеличении оптимального значения переменной на единицу.
В этом легко убедиться на практике. Оптимальное значение производства полиуретана в январе – 60 тонн, а суммарные затраты равны 4 776,45 тыс. рублей. Если в качестве оптимального значения за январь подставить число 61 и пересчитать суммарные затраты, то получим новое значение – 4 805,50. Разность этих чисел как раз и равна 29,05 – целевому коэффициенту при переменной объема производства в январе.
Широко известны и другие постановки задач динамического программирования. Некоторые из них (модель замены оборудования и модель инвестиций) будут рассмотрены на практических занятиях.

Линейное программирование - один из первых и наиболее подробно изученных разделов математического программирования. Именно линейное программирование явилось тем разделом, с которого начала развиваться сама дисциплина «математическое программирование». Термин «программирование» в названии дисциплины ничего общего с термином «программирование (т.е. составление программ) для ЭВМ» не имеет, так как дисциплина «линейное программирование» возникла еще до того времени, когда ЭВМ стали широко применяться при решении математических, инженерных, экономических и др. задач. Термин «линейное программирование» возник в результате неточного перевода английского «linear programming». Одно из значений слова «programming» - составление планов, планирование. Следовательно, правильным переводом «linear programming» было бы не «линейное программирование», а «линейное планирование», что более точно отражает содержание дисциплины. Однако, термин линейное программирование, нелинейное программирование и т.д. в нашей литературе стали общепринятыми.

Итак, линейное программирование возникло после Второй Мировой Войны и стал быстро развиваться, привлекая внимание математиков, экономистов и инженеров благодаря возможности широкого практического применения, а так же математической «стройности».

Можно сказать, что линейное программирование применимо для построения математических моделей тех процессов, в основу которых может быть положена гипотеза линейного представления реального мира: экономических задач, задач управления и планирования, оптимального размещения оборудования и пр.

Задачами линейного программирования называются задачи, в которых линейны как целевая функция, так и ограничения в виде равенств и неравенств. Кратко задачу линейного программирования можно сформулировать следующим образом: найти вектор значений переменных, доставляющих экстремум линейной целевой функции при m ограничениях в виде линейных равенств или неравенств.

Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи:

• · рационального использования сырья и материалов; задачи оптимизации раскроя;
• · оптимизации производственной программы предприятий;
• · оптимального размещения и концентрации производства;
• · составления оптимального плана перевозок, работы транспорта;
• · управления производственными запасами;
• · и многие другие, принадлежащие сфере оптимального планирования.

Так, по оценкам американских экспертов, около 75% от общего числа применяемых оптимизационных методов приходится на линейное программирование. Около четверти машинного времени, затраченного в последние годы на проведение научных исследований, было отведено решению задач линейного программирования и их многочисленных модификаций.

Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например:

• · количество продукции - расход сырья
• · количество продукции - качество продукции

Выбор компромиcного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.

При постановке задачи оптимизации необходимо:

1. Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого. Приведем примеры.

Типичный пример неправильной постановки задачи оптимизации:

«Получить максимальную производительность при минимальной себестоимости».

Ошибка заключается в том, что ставится задача поиска оптимальности 2-х величин, противоречащих друг другу по своей сути.

Правильная постановка задачи могла быть следующая:

• а) получить максимальную производительность при заданной себестоимости;
• б) получить минимальную себестоимость при заданной производительности;

В первом случае критерий оптимизации - производительность, а во втором - себестоимость.

• 2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта.
• 3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.
• 4. Учет ограничений.

Обычно оптимизируемая величина связана с экономичностью работы рассматриваемого объекта (аппарат, цех, завод). Оптимизируемый вариант работы объекта должен оцениваться какой-то количественной мерой - критерием оптимальности.

Критерием оптимальности называется количественная оценка оптимизируемого качества объекта.

На основании выбранного критерия оптимальности составляется целевая функция, представляющая собой зависимость критерия оптимальности от параметров, влияющих на ее значение. Вид критерия оптимальности или целевой функции определяется конкретной задачей оптимизации.

Таким образом, задача оптимизации сводится к нахождению экстремума целевой функции.

В зависимости от своей постановки, любая из задач оптимизации может решаться различными методами, и наоборот - любой метод может применяться для решения многих задач. Методы оптимизации могут быть скалярными (оптимизация проводится по одному критерию), векторными (оптимизация проводится по многим критериям), поисковыми (включают методы регулярного и методы случайного поиска), аналитическими (методы дифференциального исчисления, методы вариационного исчисления и др.), вычислительными (основаны на математическом программировании, которое может быть линейным, нелинейным, дискретным, динамическим, стохастическим, эвристическим и т.д.), теоретико-вероятностными, теоретико-игровыми и др. Подвергаться оптимизации могут задачи как с ограничениями, так и без них.

Экономико-математическая модель любой задачи линейного программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать; ограничения в виде системы линейных уравнений или неравенств; требование неотрицательности переменных.

В общем виде модель записывается следующим образом:

Целевая функция:

При этом aij, bi, cj () - заданные постоянные величины.

Задача состоит в нахождении оптимального значения функции (1.1) при соблюдении ограничений (1.2) и (1.3).

Систему ограничений (1.2) называют функциональными ограничениями задачи, а ограничения (1.3) - прямыми.

Вектор, удовлетворяющий ограничениям (1.2) и (1.3), называется допустимым решением (планом) задачи линейного программирования. План, при котором функция (1.1) достигает своего максимального (минимального) значения, называется оптимальным.

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

МОДЕЛЬ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

1 Математическое описание модели линейного программирования

2 Методы реализации моделей линейного программирования

3 Двойственная задача линейного программирования

Модель линейного программирования (ЛП) имеет место, если в исследуемой системе (объекте) ограничения на переменные и целевая функция линейны .

Модели ЛП используются для решения двух основных типов прикладных задач:

1) оптимального планирования в любых сферах человеческой деятельности – социальной, экономической, научно-технической и военной. Например, при оптимальном планировании производства: распределении финансовых, трудовых и других ресурсов, снабжении сырьем, управлении запасами и т. д.

2) транспортной задачи (нахождение оптимального плана различного рода перевозок, оптимального плана распределения разных средств по объектам различного назначения и т. п.)

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Требуется найти неотрицательные значения переменных

удовлетворяющих линейным ограничениям в виде равенств и неравенств

,

где – заданные числа,

и обеспечивающих экстремум линейной целевой функции

,

где – заданные числа, что записывается в виде

Допустимым решением называется любая совокупность , удовлетворяющих условиям.

Область допустимых решений – множество всех допустимых решений.

Оптимальное решение
, для которого .

Замечания

1. Приведенная модель ЛП является общей . Различают также стандартные и канонические формы моделей ЛП.

2. Условия существования реализации модели ЛП:

– множество допустимых решений – не пустое;

– целевая функция ограничена на (хотя бы сверху при поиске максимума и снизу при поиске минимума).

3.ЛП основывается на двух теоремах

Теорема 1. Множество G , определяемое системой ограничений вида, есть выпуклое замкнутое множество (выпуклый многогранник в с угловыми точками - вершинами .)

Теорема 2. Линейная форма , определенная на выпуклом многограннике

j =1,2,…,s

i=s +1,s+2,…,m ,

достигает экстремума в одной из вершин этого многогранника.

Данная теорема получила название теоремы об экстремуме линейной формы.

В соответствии с теоремой Вейерштрасса оптимальное решение единственно и является глобальным экстремумом.

Существует общий аналитический подход к реализации модели ЛП – симплекс-метод. При решении задач линейного программирования достаточно часто решения нет. Это происходит по следующим причинам.

Первую причину проиллюстрируем примером

Про такую причину говорят, что ограничения несовместны. Область допустимых решений – пустое множество.

Вторая причина комментируется следующим примером:

В данном случае, область допустимых решений не ограничена сверху. Область допустимых решений не ограничена.

Следуя традициям линейного программирования, дадим задаче ЛП экономическую интерпретацию. Пусть в нашем распоряжении имеется m типов ресурсов. Количество ресурса типа j равно . Эти ресурсы необходимы для производства n типов товаров. Обозначим количество этих товаров символами соответственно. Единица товара типа i стоит . Производство товаров типа i должно быть ограничено величинами соответственно. На производство единицы товара типа i расходуется ресурса типа j . Необходимо определить такой план производства товаров (), чтобы их суммарная стоимость была минимальной.

Задачи линейного программирования, используемые для оптимизации функционирования реальных объектов, содержат значительное число переменных и ограничений. Это обуславливает невозможность решения их графическими методами. При большом числе переменных и ограничений применяются алгебраические методы, в основе которых лежат итерационные вычислительные процедуры. В линейном программировании разработано множество алгебраических методов, различающихся между собой способами построения начального допустимого решения и условиями перехода от одной итерации к другой. Однако все эти методы базируются на общих теоретических положениях.

Общность основных теоретических положений приводит к тому, что алгебраические методы решения задач линейного программирования во многом сходны между собой. В частности, практически любой из них требует предварительного приведения задачи линейного программирования к стандартной (канонической) форме.

Алгебраические методы решения задачи ЛП начинаются с приведения ее к стандартной (канонической) форме :

,

,

i =1,..,n ; j =1,..,m .

Любая задача линейного программирования может быть приведена к стандартной форме. Сравнение общей модели с канонической моделью позволяет сделать вывод о том, что для приведения задачи ЛП к стандартной форме необходимо, во-первых, от системы неравенств перейти к равенствам, а во-вторых, преобразовать все переменные так, чтобы они были неотрицательными.

Переход к равенствам осуществляется прибавлением к левой части ограничений неотрицательной остаточной переменной для неравенств типа , и вычитанием из левой части неотрицательной избыточной переменной для неравенств типа . Например, неравенство при переходе к стандартной форме преобразуется в равенство , a неравенство - в равенство . При этом, как остаточная переменная , так и избыточная переменная являются неотрицательными.

Предполагается, что правая часть неравенств неотрицательна. В противном случае, этого можно добиться умножением обеих частей неравенства на «-1» и сменой его знака на противоположный.

Если в исходной задаче линейного программирования переменная не ограничена в знаке, ее можно представить в виде разности двух неотрицательных переменных , где .

Важной особенностью переменных является то, что при любом допустимом решении только одна из них может принимать положительное значение. Это означает, что если , то и наоборот. Следовательно, может рассматриваться как остаточная, а - как избыточная переменные.

Пример Пусть дана задача линейного программирования:

,

.

Необходимо привести ее к стандартной форме. Заметим, что первое неравенство исходной задачи имеет знак , следовательно, в него необходимо ввести остаточную переменную . В результате получим .

Второе неравенство имеет знак и для преобразования к стандартной форме требует введения избыточной переменной , выполнив эту операцию, получим .

Кроме того, переменная не ограничена в знаке. Следовательно, как в целевой функции, так и в обоих ограничениях она должна быть заменена на разность . Выполнив подстановку, получим задачу линейного программирования в стандартной форме, эквивалентную исходной задаче:

.

Задача линейного программирования, записанная в стандартной форме, представляет собой задачу поиска экстремума целевой функции на множестве векторов, являющихся решениями системы линейных уравнений с учетом условий неотрицательности. Как известно, система линейных уравнений может не иметь решений, иметь единственное решение или иметь бесконечное множество решений. Оптимизация целевой функции возможна только в том случае, если система имеет бесконечное множество решений. Система линейных уравнений имеет бесконечное множество решений, если она совместна (ранг основной матрицы равен рангу расширенной) и, если ранг основной матрицы меньше числа неизвестных.

Пусть ранг матрицы системы ограничений равен m . Это значит, что матрица имеет хоть один минор m -го порядка не равный нулю. Не нарушая общности, можно предположить, что минор расположен в левом верхнем углу матрицы. Этого всегда можно добиться, изменив нумерацию переменных. Этот не равный нулю минор ранга m принято называть базисным. Составим систему из первых m уравнений системы, записав ее следующим образом:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ - математические модели решения экономических задан, представленные в форме задач линейного программирования. Целевая функция, связи и в такой модели выражены в виде линейных уравнений.

Экономика и право: словарь-справочник. - М.: Вуз и школа . Л. П. Кураков, В. Л. Кураков, А. Л. Кураков . 2004 .

Смотреть что такое "МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ" в других словарях:

Математические модели решения экономических задач, представленные в форме задач линейного программирования. Целевая функция, связи и ограничения в такой модели выражены в виде линейных соотношений. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б … Экономический словарь

модели линейного программирования - математические модели решения экономических задач, представленные в форме задач линейного программирования. Целевая функция, связи и ограничения в такой модели выражены в виде линейных соотношений … Словарь экономических терминов

МОДЕЛЬ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ В МЕНЕДЖМЕНТЕ - вид модели, который применяют для определения оптимального способа распределения дефицитных ресурсов при наличии конкурирующих потребностей. Некоторые типичные применения этого метода в управлении производством: планирование ассортимента изделий; … Большой экономический словарь

Модели в экономике используются начиная с 18 в. В «Экономических таблицах» Ф. Кенэ, которые К. Маркс назвал идеей «...бесспорно самой гениальной из всех, какие только выдвинула до сего времени политическая экономия» (Маркс К. и Энгельс Ф., Соч.,… …

I Модели в биологии применяются для моделирования (См. Моделирование) биологических структур, функций и процессов на разных уровнях организации живого: молекулярном, субклеточном, клеточном, органно системном, организменном и популяционно … Большая советская энциклопедия

Модели экономических объектов или процессов, при описании которых используются математические средства. Цели создания Э. м. м. разнообразны: они строятся для анализа тех или иных предпосылок и положений экономической теории, логического… … Большая советская энциклопедия

- (scarcity) Свойство (товаров или производственных факторов), состоящее в том, что при нулевой цене спрос на них (по сравнению с предложением) будет чрезмерно высоким. Это значит, что в условиях равновесия цена дефицитного товара или фактора… … Экономический словарь

Построение, разработка и приложения математич. моделей принятия оптимальных решений. Содержанием теоретич. аспекта И. о. являются анализ и решение математич. задач выбора в заданном множестве допустимых решений Xэлемента, удовлетворяющего тем или … Математическая энциклопедия

- (НИР и ОКР, applied research, research and development R D) – научные исследования, направленные на решение социально практических проблем. Наука (science) сфера человеческой деятельности, функцией которой является выработка и теоретическая… … Википедия

Математическая дисциплина, предметом к рой являются модели экономич. объектов и процессов и методы их исследования. Однако понятия, результаты, методы М. э. удобно и принято излагать в тесной связи с их экономич. происхождением, интерпретацией и… … Математическая энциклопедия

Книги

• Экономико-математические методы и модели в коммерческой деятельности. Учебник , Г. П. Фомин. В учебнике рассмотрены операции, экономические показатели, схема образования прибыли, структура связи экономических и математических методов, методы и модели изучения, анализа и…
• Методы и модели оптимизации управленческих решений. Учебное пособие , А. Р. Урубков, И. В. Федотов. В учебном пособии изложены принципы оптимизации управленческих решений на основе методов и моделей линейного программирования. На примерах реальных бизнес-ситуаций показано, как, используя…